-
Lesson 5 Prefix Sums MinVagTwoSlice 나만의 풀이알고리즘/codility 2021. 6. 4. 23:53
문제
A non-empty array A consisting of N integers is given. A pair of integers (P, Q), such that 0 ≤ P < Q < N, is called a slice of array A (notice that the slice contains at least two elements). The average of a slice (P, Q) is the sum of A[P] + A[P + 1] + ... + A[Q] divided by the length of the slice. To be precise, the average equals (A[P] + A[P + 1] + ... + A[Q]) / (Q − P + 1).
For example, array A such that:
A[0] = 4 A[1] = 2 A[2] = 2 A[3] = 5 A[4] = 1 A[5] = 5 A[6] = 8
contains the following example slices:
slice (1, 2), whose average is (2 + 2) / 2 = 2;slice (3, 4), whose average is (5 + 1) / 2 = 3;slice (1, 4), whose average is (2 + 2 + 5 + 1) / 4 = 2.5.
The goal is to find the starting position of a slice whose average is minimal.
Write a function:
def solution(A)
that, given a non-empty array A consisting of N integers, returns the starting position of the slice with the minimal average. If there is more than one slice with a minimal average, you should return the smallest starting position of such a slice.
For example, given array A such that:
A[0] = 4 A[1] = 2 A[2] = 2 A[3] = 5 A[4] = 1 A[5] = 5 A[6] = 8
the function should return 1, as explained above.
Write an efficient algorithm for the following assumptions:
N is an integer within the range [2..100,000];each element of array A is an integer within the range [−10,000..10,000].대충 해석하자면
비어있지 않은 A에 N개의 정수가 주어지는데 P부터 Q까지 구간합 중 평균에서 가장 작은 P를 리턴하는 것이다.
첫 번째 시도
코드를 날려먹었다...
대충 전체 구간 합의 나머지를 구했더니 당연하게도 제곱으로 나왔다.
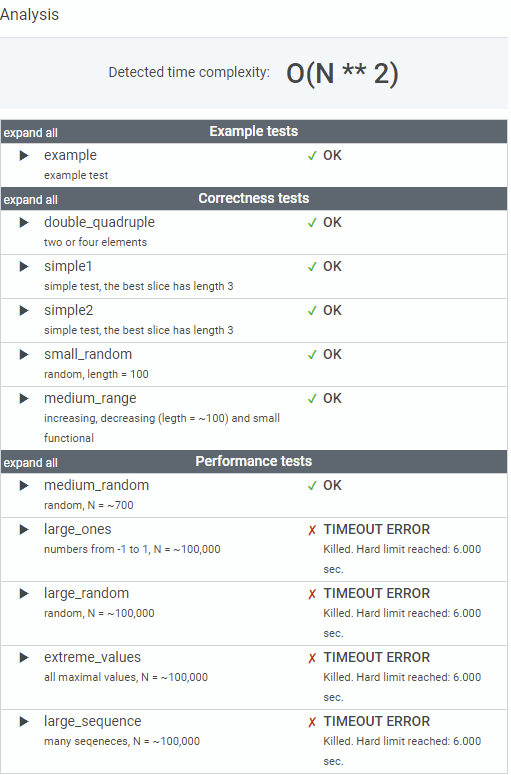
2시간째 시도한 결과 포기
알고리즘을 알아야 푸는 문제였다... 이런 수학적 지식이 있어야 푸는 건 너무하지 않나 싶다.
아래와 같이 2,3개인 경우에만 고려하는 어이없는 문제
구간 합조 차 사용하지 않아도 되는 문제다.

알고리즘 def solution(A): min_val = (A[0]+A[1])/2 min_index = 0 for i in range(2, len(A)): val = (A[i-2]+A[i-1]+A[i])/3 if val<min_val: min_val = val min_index = i-2 val = (A[i-1]+A[i])/2 if val<min_val: min_val = val min_index = i-1 return min_index
O(N) '알고리즘 > codility' 카테고리의 다른 글
Lesson 5 Prefix Sums PassingCars 나만의 풀이 (0) 2021.06.02 Lesson 4 Counting Elements PermCheck 나만의풀이 (0) 2021.06.02 Lesson 4 Counting Elements MaxCounters 나만의풀이 (0) 2021.05.31 Lesson 4 Counting Elements FrogRiverOne 나만의풀이 (0) 2021.05.30 Codility Lesson 3 TapeEquilibrium 나만의 풀이 (0) 2021.05.30